Calibration of All-Sky/Telescopic Images to Rayleighs

Using Standard Stars

 

Jody Wilson

April 12, 2001

 

 

This report describes a method of calibrating surface brightnesses in a telescopic or all-sky image using standard stars.

 

Given:

 

-Flux of standard star at the Earth in photons cm-2 s-1 Å-1 for the wavelength observed (look up in standard star files)

-Total detected brightness (S) of standard star image in Data Numbers (DN)

-Spectral width of the filter in Angstroms (approximately FWHM ´ peak transmission)

-Solid angle θ2 of a pixel in radians (for telescopic images only)

 

 

Step 1: Calculate airless star flux seen by instrument (F).

 

The airless flux F is the spectral flux (photons cm-2 s-1 Å-1 from table) multiplied by the filter's spectral width:

 

F = (spectral flux) ´ (spectral width) (1)

 

This is the flux from the standard star that the instrument would see of there was no attenuation of the starlight by the Earth’s atmosphere.

 

 

 

Step 2: Calculate the apparent airless omnidirectional surface brightness of the standard star image (I).

 

Assume that the standard star has an angular size of exactly one pixel, that it is emitting isotropically, and that it is at some arbitrary distance R from the telescope.

 

 


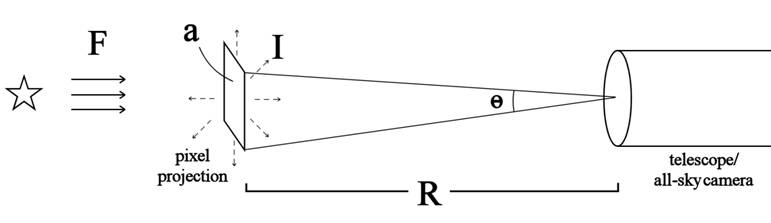
The area a of the “star pixel” is then

 

a = (Rθ)2,                                                       (2)

 

where θ is the angular width of one pixel in radians. We may now define an omnidirectional surface brightness I (units of photons cm-2 s-1) of this star pixel such that its total brightness (in photons s-1) is Ia. Now the flux F from the star pixel in any direction at a distance R can be expressed as the product of the star pixel’s total brightness divided by the area of a sphere of radius R:

 

F = Ia/(4πR2).                                                        (3)

 

This is the same flux calculated in step 1. Substituting for a from equation (2):

 

F = I θ2/ 4π.                                                       (4)

 

Solving for I (photons cm-2 s-1):

 

I = 4πF /θ2

 

One Rayleigh is 106 photons cm-2 s-1, so we finally have:

 

IRayleighs = [4πF /θ2] ´ [10-6 Rayleighs/(photon cm-2 s-1)]               (5)

 

 

 

 

Step 3: Calibrate the image.

 

3A: Telescopic images

 

Given a standard star of measured brightness S and apparent surface brightness I with an exposure time t1, and a second image with exposure time t2 to be calibrated, the pixel-by-pixel brightness in Rayleighs of the image is given by

 

                            imageRayleighs = imageDN · (t1/t2) · (I/S)                                     (6)

 

 

3B: All-sky images

 

All-sky images have three characteristics which make them more difficult to calibrate than telescopic images:

 

1.     The angular size of a pixel depends on its location in the image.

 

2.     Some all-sky images cannot be flat-fielded, so any center-to-edge changes in instrument sensitivity are unknown.

 

3.     All airmasses from 1 to >10 are represented in a single image, so an “airless” calibration for one part of an image does not apply to other parts.

 

So calibration of all-sky images with standard stars requires calculating the solid angle ωpixel of each pixel in the image. For telescopic images this is simply θ2 in equation (5), but pixel projections are warped in all-sky images. Once the solid angle of each pixel is known, the other two problems above (2 and 3) are solved by measuring standard stars at several zenith angles.

 

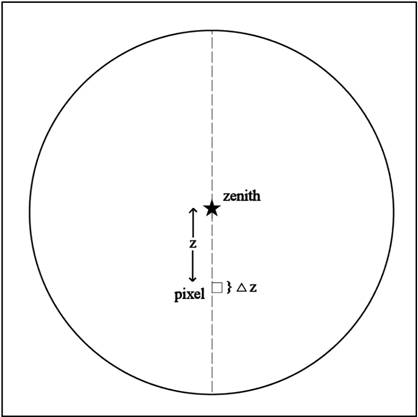
Consider a pixel in an all-sky image at a distance of r pixels from the zenith.

 


The true zenith distance of this pixel can be represented as a function of its pixel distance r. This function, z(r), is determined by measuring star locations and fitting a function to the zenith distances at the time the image was taken.

 

Once z(r) is known, the latitudinal size of a pixel on the meridian is easily calculated:

 

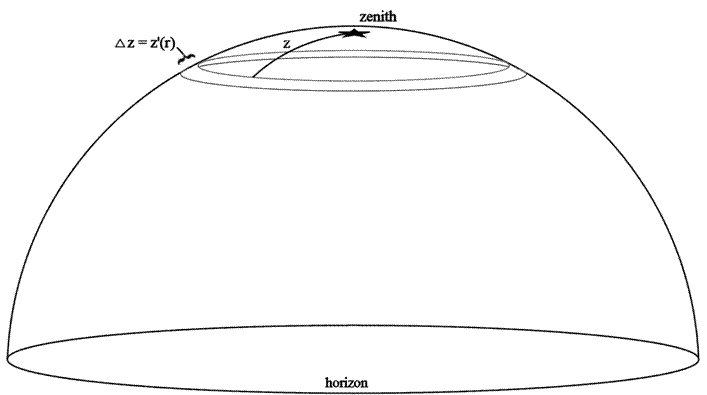
Δz = |z(r) – z(r+1)| = z'(r).                                                   (7)

 

 


Consider an annulus of radius r pixels and thickness of one pixel. Its total area in pixels is

 

A(r) = 2πr                                                              (8)


 

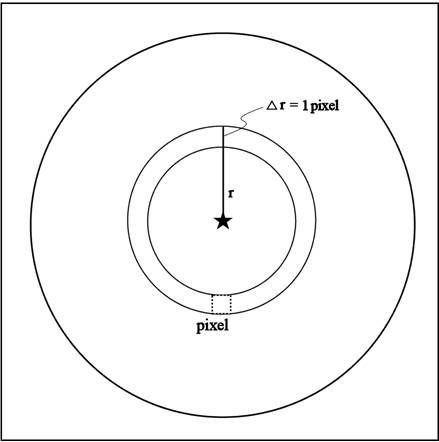
The angular circumference of this annulus is 360º sin(z), so the solid angle of the annulus is:

 

Ω(r) = 360º sin[z(r)] z'(r).                                            (9)

 

 


Thus the solid angle of each pixel in the annulus is, from equations (8) and (9):

 

ωpixel(r) = Ω(r)/A(r) = 180º sin[z(r)] z'(r)/(π r)               (10)

 

Now substituting ωpixel(r) for θ2 in equation (5), the apparent brightness in Rayleighs of any standard star in the all-sky image can be calculated. Several standard stars should be measured (or one standard star at several zenith angles) in order to determine how the DN-to-Rayleigh conversion factor (equation 6) varies with r as a result of atmospheric extinction and varying sensitivity of the system (flat field issues).